In recent years, it had been an evolution in the sensors used by vision systems. Different technologies from RGB camera, IR-camera, LIDAR, RADAR, or sensor combinations can work in different spectrum bands. A new alternative to the vision system is the single-pixel camera (SPC), an architecture based on the compressive sensing theory for 2D reconstruction images. SPC's feature is used as the single detector that measures the linear combinations of pixels through patterns projection of structured light over the object that would like to photograph instead of using an array of pixels as in RGB sensors or cameras. These architectures offer the advantage that they can be adapted to different spectrum bands as near-infrared (NIR), and could operate in scenarios with low visibility or under rain, mist, or fog conditions. Currently, there is little information that discusses the problem of spatial resolution in SPC in scattering conditions for which we defined a methodology to evaluate the spatial resolution SPC's in terms of point spread function (PSF), and we analyzed how it affected the spatial resolution with the distance and under foggy conditions, for an SPC with active illumination at the wavelength at 1550 nm.

Fig.1. Spatial resolution using Hilbert Scanning at 20 cm , with separation between x=10 mm and y=10 mm ∆x=11.6 mm and ∆y=12 mm without Fog (a-b), and ∆x=16 mm and ∆y=18 mm with Fog (c-d).
SCATTERING EFFECT

When light interacts with a water particle in the air, various physical phenomena occur as reflection, refraction, absorption, and scattering. The scattering is related to the particle size (sp), defined as: sp=πD/λ , where D is the particle diameter, and λ the incident
Fig.2 .I ncident beam scattering characteristics for
different particles size: a) Rayleigh regime λ >> D,
b) Mie regime λ∼D and c) Ray optical regime λ << D
photon wavelength. This scattering process is respectively related to the size of the particle. For small
scattering particles (see Fig. 2a), the distribution of scattered light is symmetric in the forward and backward directions. If the particle size increases, the scattered energy increases in the direction of the incident beam diminishing the amount of scattered light in the opposite direction (see Fig. 2b, 2c).
The scattering cross-section Qd is proportional to the radiation-particle interaction probability, and it is defined through the so-called effective area of the collision. For which the total scattering of the impinging light is proportional to the effect cross-section (Mie theory) multiplied by the amount of the particles present in the medium. The scattering cross-section is here related tospof the inter-acting particle through the probability of extinction of the photon, also known as the extinction efficiency, Qext, the scattering probability Qsca, and the absorption probability Qabs.
FOG EFFECT IN THE SPATIAL RESOLUTION

In scattering scenarios, present changes in the level of contrast in the scenes that affect the quality of the reconstructed 2D image, and deducting spatial resolution image. In the case of scenarios with fog the level contrast is defined by Beer–Lambert law , where the contrast decreases by an exponential factor with distance defined by Eq.(1), with β as scattering coefficients Eq.(2), and depend on Qsc is the scattering coefficient (calculate using matlab ), the radius of particles r andDdensityis the density of particles suspended in the medium.
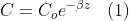
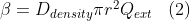
Therefore, as the measurement distance increases, the SPC's ability for discriminate objects is reduced due to this scattering effect.

Fig.3 .NIR-SPI test image circle of 50 diameter: At focal length distance d1=18 cm, and d2=30 cm , a-e) basic scanning, b-f) Hilbert scanning, c-g) Zig-Zag scanning, d-h) Spiral scanning.

Fig.4.NIR-SPI test image circle under foggy conditions of 50 diameter: At focal length distance d1=18 cm, and d2=30 cm, a-e) basic scanning, b-f) Hilbert scanning, c-g) Zig-Zag scanning, d-h) Spiral scanning.
Comments